Absorption band

In quantum mechanics, an absorption band is a range of wavelengths, frequencies or energies in the electromagnetic spectrum that are characteristic of a particular transition from initial to final state in a substance.
According to quantum mechanics, atoms and molecules can only hold certain defined quantities of energy, or exist in specific states.[1] When such quanta of electromagnetic radiation are emitted or absorbed by an atom or molecule, energy of the radiation changes the state of the atom or molecule from an initial state to a final state.
Overview
[edit]When electromagnetic radiation is absorbed by an atom or molecule, the energy of the radiation changes the state of the atom or molecule from an initial state to a final state. The number of states in a specific energy range is discrete for gaseous or diluted systems, with discrete energy levels. Condensed systems, like liquids or solids, have a continuous density of states distribution and often possess continuous energy bands. In order for a substance to change its energy it must do so in a series of "steps" by the absorption of a photon. This absorption process can move a particle, like an electron, from an occupied state to an empty or unoccupied state. It can also move a whole vibrating or rotating system, like a molecule, from one vibrational or rotational state to another or it can create a quasiparticle like a phonon or a plasmon in a solid.
Electromagnetic transitions
[edit]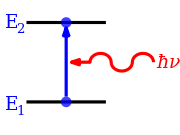
When a photon is absorbed, the electromagnetic field of the photon disappears as it initiates a change in the state of the system that absorbs the photon. Energy, momentum, angular momentum, magnetic dipole moment and electric dipole moment are transported from the photon to the system. Because there are conservation laws, that have to be satisfied, the transition has to meet a series of constraints. This results in a series of selection rules. It is not possible to make any transition that lies within the energy or frequency range that is observed.[2]
The strength of an electromagnetic absorption process is mainly determined by two factors. First, transitions that only change the magnetic dipole moment of the system are much weaker than transitions that change the electric dipole moment and that transitions to higher order moments, like quadrupole transitions, are weaker than dipole transitions. Second, not all transitions have the same transition matrix element, absorption coefficient or oscillator strength.
For some types of bands or spectroscopic disciplines temperature and statistical mechanics plays an important role. For (far) infrared, microwave and radio frequency ranges the temperature dependent occupation numbers of states and the difference between Bose-Einstein statistics and Fermi-Dirac statistics determines the intensity of observed absorptions. For other energy ranges thermal motion effects, like Doppler broadening may determine the linewidth.
Band and line shape
[edit]
A wide variety of absorption band and line shapes exist, and the analysis of the band or line shape can be used to determine information about the system that causes it. In many cases it is convenient to assume that a narrow spectral line is a Lorentzian or Gaussian, depending respectively on the decay mechanism or temperature effects like Doppler broadening.[3] Analysis of the spectral density and the intensities, width and shape of spectral lines sometimes can yield a lot of information about the observed system like it is done with Mössbauer spectra.
In systems with a very large number of states like macromolecules and large conjugated systems the separate energy levels can't always be distinguished in an absorption spectrum. If the line broadening mechanism is known and the shape of then spectral density is clearly visible in the spectrum, it is possible to get the desired data. Sometimes it is enough to know the lower or upper limits of the band or its position for an analysis.
For condensed matter and solids the shape of absorption bands are often determined by transitions between states in their continuous density of states distributions. For crystals, the electronic band structure determines the density of states. In fluids, glasses and amorphous solids, there is no long range correlation and the dispersion relations are isotropic. For charge-transfer complexes and conjugated systems, the band width is complicated by a variety of factors, compared to condensed matter.[4]
Types
[edit]Electronic transitions
[edit]Electromagnetic transitions in atoms, molecules and condensed matter mainly take place at energies corresponding to the UV and visible part of the spectrum. Core electrons in atoms, and many other phenomena, are observed with different brands of XAS in the X-ray energy range. Electromagnetic transitions in atomic nuclei, as observed in Mössbauer spectroscopy, take place in the gamma ray part of the spectrum. The main factors that cause broadening of the spectral line into an absorption band of a molecular solid are the distributions of vibrational and rotational energies of the molecules in the sample (and also those of their excited states). In solid crystals the shape of absorption bands are determined by the density of states of initial and final states of electronic states or lattice vibrations, called phonons, in the crystal structure. In gas phase spectroscopy, the fine structure afforded by these factors can be discerned, but in solution-state spectroscopy, the differences in molecular micro environments further broaden the structure to give smooth bands. Electronic transition bands of molecules may be from tens to several hundred nanometers in breadth.
Vibrational transitions
[edit]Vibrational transitions and optical phonon transitions take place in the infrared part of the spectrum, at wavelengths of around 1-30 micrometres.[5]
Rotational transitions
[edit]Rotational transitions take place in the far infrared and microwave regions.[6]
Other transitions
[edit]Absorption bands in the radio frequency range are found in NMR spectroscopy. The frequency ranges and intensities are determined by the magnetic moment of the nuclei that are observed, the applied magnetic field and temperature occupation number differences of the magnetic states.
Applications
[edit]Materials with broad absorption bands are being applied in pigments, dyes and optical filters. Titanium dioxide, zinc oxide and chromophores are applied as UV absorbers and reflectors in sunscreen.
Absorption bands of interest to the atmospheric physicist
[edit]In oxygen:
- the Hopfield bands, very strong, between about 67 and 100 nanometres in the ultraviolet (named after John J. Hopfield);
- a diffuse system between 101.9 and 130 nanometres;
- the Schumann–Runge continuum, very strong, between 135 and 176 nanometres;
- the Schumann–Runge bands between 176 and 192.6 nanometres (named for Victor Schumann and Carl Runge);
- the Herzberg bands between 240 and 260 nanometres (named after Gerhard Herzberg);
- the atmospheric bands between 538 and 771 nanometres in the visible spectrum; including the oxygen δ (~580 nm), γ (~629 nm), B (~688 nm), and A-band (~759-771 nm)[7]
- a system in the infrared at about 1000 nanometres.[8]
In ozone:
- the Hartley bands between 200 and 300 nanometres in the ultraviolet, with a very intense maximum absorption at 255 nanometres (named after Walter Noel Hartley);
- the Huggins bands, weak absorption between 320 and 360 nanometres (named after Sir William Huggins);
- the Chappuis bands (sometimes misspelled "Chappius"), a weak diffuse system between 375 and 650 nanometres in the visible spectrum (named after J. Chappuis); and
- the Wulf bands in the infrared beyond 700 nm, centered at 4,700, 9,600 and 14,100 nanometres, the latter being the most intense (named after Oliver R. Wulf).
In nitrogen:
- The Lyman–Birge–Hopfield bands, sometimes known as the Birge–Hopfield bands, in the far ultraviolet: 140– 170 nm (named after Theodore Lyman, Raymond T. Birge, and John J. Hopfield)
See also
[edit]References
[edit]- ^ Ning, Yong-Cheng (2011-04-18). "Interpretation of Infrared Spectra". Interpretation of Organic Spectra. John Wiley & Sons. ISBN 978-0-470-82831-1.
- ^ Dolgaleva, Ksenia (2022-05-31). Introduction to Optics I: Interaction of Light with Matter. Springer Nature. pp. 50–55. ISBN 978-3-031-02387-3.
- ^ Hollas, M.J. (1996). Modern Spectroscopy (3rd ed.). Wiley. pp. 30–34. ISBN 0471965227.
- ^ Autschbach, Jochen (November 2007). "Why the Particle-in-a-Box Model Works Well for Cyanine Dyes but Not for Conjugated Polyenes". Journal of Chemical Education. 84 (11): 1840. doi:10.1021/ed084p1840. ISSN 0021-9584.
- ^ Edgar Bright Wilson, J.C. Decius, Paul C. Cross, MOLECULAR VIBRATIONS. The Theory of Infrared and Raman Vibrational Spectra. McGraw-Hill, New York, 1955
- ^ Harry C. Allen Jr., Paul C. Cross, Molecular Vib-Rotors. THE THEORY AND INTERPRETATION OF HIGH RESOLUTION INFRARED SPECTRA. John Wiley and Sons, Inc. New York, 1963
- ^ David A. Newnham and John Ballard. Visible absorption cross sections and integrated absorption intensities of molecular oxygen (O2 and O4). http://onlinelibrary.wiley.com/doi/10.1029/98JD02799/pdf
- ^ K.M Smith, D.A Newnham. Near-infrared absorption spectroscopy of oxygen and nitrogen gas mixtures. doi:10.1016/S0009-2614(99)00584-9
